|
Το φαινόμενο κατά το οποίο
εκπέμπονται ηλεκτρόνια από τα μέταλλα όταν αυτά θερμαίνονται ονομάζεται
θερμιονική εκπομπή ηλεκτρονίων. Τα ηλεκτρόνια αυτά υπάρχουν στο εσωτερικό του
μετάλλου και κυκλοφορούν ανάμεσα στα θετικά ιόντα του κρυσταλλικού πλέγματος
δίνοντας την εικόνα κλασσικών σωματιδίων αερίου περιορισμένων σε χώρο που
ορίζεται από τις επιφάνειες του μετάλλου.
Τα
ηλεκτρόνια είναι κβαντικά σωματίδια και αυτό έχει ως συνέπεια οι ενέργειές τους
να κατανέμονται με ασυνεχή τρόπο. Επίσης
λόγω της απαγορευτικής αρχής Pauli
τα ηλεκτρόνια καταλαμβάνουν ανά δύο ενεργειακές στάθμες, από την χαμηλότερη ως
μια ορισμένη υψηλότερη μέχρι να κατανεμηθούν όλα. Η υψηλότερη ενεργειακή στάθμη
στη θερμοκρασία του απόλυτου μηδενός καλείται ενέργεια Fermi ΕF
και είναι
χαρακτηριστική για κάθε στοιχείο. Τα χαρακτηριστικά αυτά καθιστούν ακατάλληλα
τα μοντέλα κατανομής ενέργειας αερίων. Αποδεικνύεται ότι τα ηλεκτρόνια
ακολουθούν τη στατιστική Fermi–Dirac (F-D):
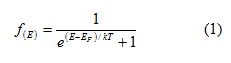
Όπου k=1.3807·10-23J·K-1 η σταθερά Boltzmann και
T
η
θερμοκρασία σε Kelvin.
Καθώς
θερμαίνεται το σώμα του μετάλλου σε υψηλές θερμοκρασίες τα ηλεκτρόνια αποκτούν
μέση θερμική ενέργεια kT. Η ενέργεια αυτή είναι χαμηλή
ακόμα και σε θερμοκρασίες κοντά στη θερμοκρασία τήξης του μετάλλου. Ορισμένα
ηλεκτρόνια όμως στην ουρά της κατανομής F-D έχουν
ικανή ενέργεια ώστε να μπορέσουν να φύγουν από το μέταλλο. Το ελάχιστο έργο που
χρειάζεται ώστε τα ηλεκτρόνια με την υψηλότερη ενεργειακή στάθμη να διαπεράσουν
το φράγμα δυναμικού V0 που αποτελούν οι
επιφάνειες του μετάλλου ονομάζεται έργο
εξόδου φ και είναι χαρακτηριστικό για κάθε μέταλλο. Ισούται με το φράγμα
δυναμικού μείον την ενέργεια Fermi.

Η εκπομπή
των ηλεκτρονίων από το σώμα μετάλλων μπορεί να μελετηθεί σε κατάλληλες
διατάξεις. Μια από αυτές είναι η ηλεκτρονική λυχνία κενού. Η πιο απλή (δίοδος)
αποτελείται από μια μεταλλική πλάκα (κάθοδος) που θερμαίνεται μέσω ενός σύρματος
βολφραμίου το οποίο διαρρέεται από ρεύμα και ένα ηλεκτρόδιο ανόδου, το οποίο
συλλέγει τα ηλεκτρόνια που εκπέμπονται από την κάθοδο λόγω διαφοράς δυναμικού
που εφαρμόζεται μεταξύ ανόδου-καθόδου με ηλεκτροθετικότερη την άνοδο. Σε μικρές
διαφορές δυναμικού μόνο τα υψηλότερα ενεργειακά ηλεκτρόνια (από την κατανομή F-D) καταφέρνουν να φτάσουν στην άνοδο και
αποτελούν το ανοδικό ρεύμα IA. Αυξάνοντας
προοδευτικά την ανοδική τάση VA, όλο και
περισσότερα ηλεκτρόνια συλλέγονται από την άνοδο αυξάνοντας έτσι το ανοδικό
ρεύμα μέχρι μια ορισμένη μέγιστη τιμή (ρεύμα κόρου IK)
που εξαρτάται από τη θερμοκρασία καθόδου. Είναι προφανές, ότι συμβαίνει αυτό
γιατί όταν εμφανίζεται το ρεύμα κόρου όλα τα παραγόμενα ηλεκτρόνια από την
κάθοδο συλλέγονται στην άνοδο και δεν είναι δυνατό να αυξηθούν όσο και αν
αυξηθεί η τάση ανόδου κρατώντας σταθερή τη θερμοκρασία καθόδου.
Για την
ισχυρή εξάρτηση του ρεύματος κόρου από τη θερμοκρασία της καθόδου προτάθηκε από
τον Richardson μια
εμπειρική σχέση:
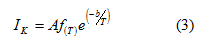
όπου Α και b είναι σταθερές χαρακτηριστικές της
καθόδου της λυχνίας και f(T)=Tn όρος εξαρτώμενος από τη θερμοκρασία μικρού
βαθμού.
Η παραπάνω
σχέση μπορεί να παραχθεί θεωρητικά με μελέτη της στατιστικής συμπεριφοράς του
ηλεκτρονικού νέφους, όπου αν λάβουμε υπ’ όψιν μας την κατανομή F-D θεωρώντας τα
ηλεκτρόνια φερμιόνια γίνεται:
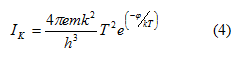
θέτοντας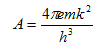 και και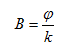 και λογαριθμίζοντας
την σχέση (4) μετά από πράξεις έχουμε: και λογαριθμίζοντας
την σχέση (4) μετά από πράξεις έχουμε:
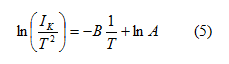
η οποία είναι μια σχέση του τύπου y=bx+a. Από την κλίση της ευθείας που
αναπαριστά μπορούμε να υπολογίσουμε το έργο εξόδου φ.
Για τις
ανάγκες του πειράματος χρησιμοποιήσαμε μια δίοδο λυχνία κενού εμμέσου θέρμανσης,
ένα τροφοδοτικό συνεχούς τάσης 0-5V για την τροφοδοσία των
νημάτων θέρμανσης της καθόδου, ένα αναλογικό βολτόμετρο περιοχής 0-5V με διαγράμμιση ανά 0.25V συνδεδεμένο στα νήματα
θέρμανσης, ένα αναλογικό αμπερόμετρο περιοχής 0-200mA με
διαγράμμιση ανά 5mA συνδεδεμένο στο κύκλωμα θέρμανσης,
ένα τροφοδοτικό συνεχούς τάσης 0-300V για τη διαφορά
δυναμικού ανόδου-καθόδου και ένα ψηφιακό αμπερόμετρο με διαβάθμιση 0.01mA για τη μέτρηση του ανοδικού ρεύματος.
Για τα νήματα θέρμανσης θεωρήθηκε ότι ο θερμικός συντελεστής
είναι σταθερός σε όλες τις θερμοκρασίες, ότι το νήμα είχε σταθερή θερμοκρασία
σε όλο το μήκος του και ότι οι κολλήσεις και οι σύνδεσμοι στο κύκλωμα θέρμανσης
είχαν μηδενική τιμή αντίστασης. Η θερμοκρασία της καθόδου δεν ήταν δυνατό να
μετρηθεί άμεσα και για αυτό το λόγο υπολογίστηκε έμμεσα με την παρακάτω μέθοδο.
Σε πρώτη προσέγγιση η αντίσταση ενός μετάλλου μεταβάλλεται με τη θερμοκρασία
γραμμικά σύμφωνα με τη σχέση:
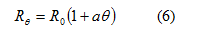
Από παλαιότερο πείραμα ήταν γνωστό ότι τα νήματα θέρμανσης στους
25οC είχαν αντίσταση:
R25=6.3Ω.
Το α ήταν γνωστό και ίσο με
a=4.5·10-3grad-1. Με βάση αυτές τις τιμές βρήκαμε από τη σχέση (6) ότι σε θερμοκρασία 0οC η αντίσταση των νημάτων R0 ήταν: R0=5.66Ω.
Από την ίδια σχέση λύνοντας ως προς τη θερμοκρασία υπολογίσαμε στη συνέχεια τη
θερμοκρασία των νημάτων:
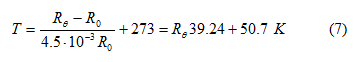
και το σφάλμα στη μέτρηση της θερμοκρασίας είναι:
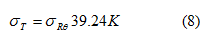
Η τιμή της Rθ
υπολογίζεται εύκολα με το νόμο του Ohm από τις τιμές τάσης Vθ και
ρεύματος Ιθ στο κύκλωμα
των νημάτων θέρμανσης:
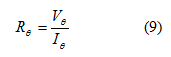
και το σφάλμα στην τιμή της αντίστασης υπολογίζεται από τη
σχέση:
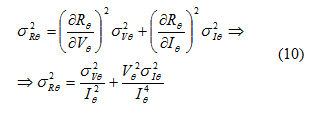
Αρχικά κάναμε ορισμένες μετρήσεις για να μελετήσουμε τα
χαρακτηριστικά της λυχνίας. Για τάση θέρμανσης Vθ=2.5V και Vθ=4V και μετά από
παραμονή αρκετής ώρας στην κάθε μια από αυτές, για όσο το δυνατό καλύτερη
σταθεροποίηση της θερμοκρασίας, καταγράψαμε τις τιμές ανοδικού ρεύματος ΙA για διάφορες τάσεις
ανόδου-καθόδου VKA από 0-300V. Παρατηρήσαμε ότι μέγιστο ρεύμα έχουμε για ανοδική τάση VKA=300V το οποίο και θεωρούμε
ρεύμα κόρου ΙK. Οι
μετρήσεις παρουσιάζονται στον πίνακα Ι. Με βάση τις μετρήσεις αυτές χαράξαμε τη
χαρακτηριστική καμπύλη της διόδου για κάθε περίπτωση.
Πίνακας Ι. Ανοδικό ρεύμα ΙΑ για διάφορες τάσεις ανόδου-καθόδου VKA με δύο διαφορετικές
τάσεις στα νήματα θέρμανσης καθόδου Vθ.


Σχήμα 1. Χαρακτηριστική καμπύλη λυχνίας
Στη συνέχεια μετρήσαμε το ρεύμα κόρου ΙΚ για διάφορες τιμές τάσης θέρμανσης Vθ μεταξύ 2.5V και 5V. Επειδή η θερμοκρασία της καθόδου θα έπαιρνε μέγιστη τιμή σε άπειρο θεωρητικά χρόνο μετά την
αποκατάσταση της τάσης θέρμανσης, κάτι που δεν ήταν δυνατό να περιμένουμε να συμβεί, οι μετρήσεις όλες έγιναν για την κάθε φορά 3 λεπτά ακριβώς μετά την αποκατάσταση της νέας τάσης θέρμανσης. Αυτό όμως αναμένεται να εισάγει ένα συστηματικό σφάλμα στους υπολογισμούς μας.
Υπολογίσαμε την ωμική αντίσταση Rθ και τη θερμοκρασία των νημάτων θέρμανσης Τ της καθόδου για την κάθε μια τάση θέρμανσης Vθ
που εφαρμόσαμε. Θεωρήσαμε ότι αυτή είναι και η θερμοκρασία καθόδου σύμφωνα με τις παραδοχές που κάναμε παραπάνω. Ανάλογα με το είδος του οργάνου που έγινε η μέτρηση θεωρήσαμε ως σφάλμα μέτρησης τη μισή τιμή της ελάχιστης υποδιαίρεση της κλίμακας του οργάνου για τα αναλογικά όργανα και μια μονάδα του λιγότερο σημαντικού ψηφίου για το ψηφιακό. Συγκεκριμένα για την τάση θέρμανσης Vθ θεωρήσαμε σφάλμα μέτρησης σVθ=0.125V, για το ρεύμα θέρμανσης Ιθ σφάλμα σΙθ=2.5mA και για το ανοδικό ρεύμα ΙΑ σφάλμα σΙΑ=0.01mA. Το σφάλμα στον υπολογισμό της αντίστασης
θέρμανσης και της θερμοκρασίας καθόδου που προέκυψε για την κάθε μέτρηση δίνεται στον πίνακα ΙΙ μαζί με τις υπόλοιπες μετρήσεις.
Πίνακας ΙΙ. Ρεύμα θέρμανσης Ιθ και ρεύμα κόρου ΙΚ που μετρήθηκαν, τιμή αντίστασης Rθ και θερμοκρασίας Τ νημάτων θέρμανσης με τα σφάλματά τους σRθi, σΤi που υπολογίσθηκαν για κάθε τάση θέρμανσης Vθ.

Από τον πίνακα ΙΙ παρατηρούμε ότι το ρεύμα κόρου ΙK αυξάνει όσο αυξάνει η θερμοκρασία καθόδου. Με βάση τις τιμές θερμοκρασίας
καθόδου Τ και ρεύματος κόρου ΙΚ του πίνακα ΙΙ και την εξίσωση (5) χαράξαμε ένα διάγραμμα του y=ln(IK/T 2) συναρτήσει του x=1/T. Οι τιμές των x και y που χρησιμοποιήσαμε και των σφαλμάτων που προκύπτουν παρουσιάζονται στον πίνακα ΙΙΙ.
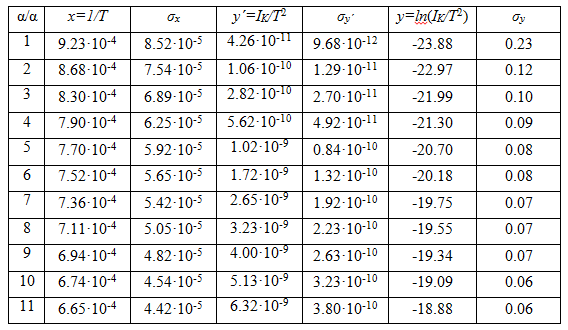
Πίνακας ΙΙΙ. Τιμές
των x=1/T και y=ln(IK/T 2) και σφαλμάτων αυτών.
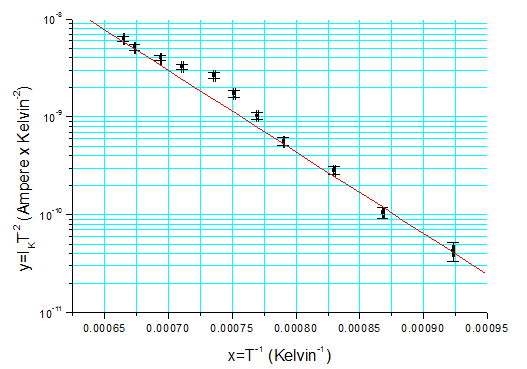
Σχήμα 2. Διάγραμμα του y=ln(IK/T 2) συναρτήσει τουx=1/T.
Στο διάγραμμα του σχήματος 2 χρησιμοποιήθηκαν οι τιμές [x=T -1, y=IKT -2] λόγω του ότι έγινε χρήση λογαριθμικής κλίμακας στην τεταγμένη, ενώ στη μέθοδο ελαχίστων τετραγώνων, παρακάτω,
χρησιμοποιήθηκαν οι τιμές [x=T -1, y=ln(IKT -2)]. Οι τιμές των σφαλμάτων για x=T -1 προέκυψαν από τη σχέση:
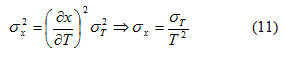
Οι τιμές των σφαλμάτων για y=IKT -2 από τη σχέση:
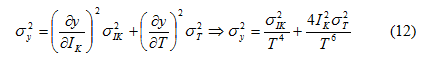
και για y=ln(IKT -2) από τη σχέση :
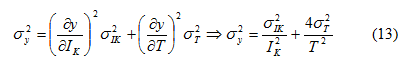
Παρατηρούμε ότι οι τιμές [x=T -1, y=IKT -2] διατάσσονται στη λογαριθμική κλίμακα σχεδόν σε ευθεία γραμμή, όπως άλλωστε περιμέναμε από την εξίσωση (5). Η εξίσωση αυτή όμως προέκυψε από
επεξεργασία της σχέσης του Richardson. Για αυτό και η διάταξη των σημείων που παρατηρείται αποτελεί πειραματική επιβεβαίωση της σχέσης του Richardson.
Με γραμμική προσαρμογή προσδιορίσαμε τη σταθερά a και την κλίση b με τα σφάλματά τους από τις τιμές [x=T -1,
y=ln(IKT -2)] για την ευθεία που προκύπτει.
Βρέθηκαν: a=(-6.1±0.8) και b=-(19049±1036). Από τις αντικαταστάσεις που κάναμε για τη σχέση (5) (και επειδή a=lnΑ και b=-B) προκύπτει ότι το έργο εξόδου είναι φ=(2.63±0.14)·10-19J=(1.64±0.09)eV. [k=1.380710-23J·K-1, eV=1.6·10-19J]
Συμπεράσματα
Από το πείραμα που εκτελέσαμε διαπιστώσαμε
ότι ο αριθμός των εκπεμπόμενων ηλεκτρονίων εξαρτάται από τη θερμοκρασία καθόδου
και αυξάνεται όσο αυξάνει αυτή. Μελετώντας στη συνέχεια το ρεύμα κόρου για
διάφορες θερμοκρασίες καθόδου αποδείξαμε πειραματικά τη σχέση του Richardson.
Με τη βοήθεια της σχέσης του Richardson στη
συνέχεια υπολογίσαμε το έργο εξόδου για το υλικό της καθόδου το οποίο βρήκαμε
να κυμαίνεται πολύ κοντά στην τιμή που αναφέρει το εγχειρίδιο του εργαστηρίου.
Σημαντική επίδραση για την ακρίβεια του αποτελέσματος έχει ο ακριβής
προσδιορισμός της θερμοκρασίας καθόδου. Για αυτό οι παραδοχές που κάναμε για τη σχέση (5) και το συστηματικό σφάλμα των οργάνων μέτρησης που αναφέραμε
πιθανόν να επηρέασαν το αποτέλεσμά μας.
|
