Ισοδύναμα κυκλώματα Norton & Thevenin

     Πολλές φορές θέλουμε να μελετήσουμε έναν κλάδο κάποιου κυκλώματος χωρίς να μας ενδιαφέρει αναλυτικά τι συμβαίνει στο υπόλοιπο κύκλωμα. Μπορούμε σε αυτήν την περίπτωση να αντικαταστήσουμε το κύκλωμα που δεν μας ενδιαφέρει με ένα ισοδύναμο, που έχει την ίδια συμπεριφορά με το αρχικό στα σημεία που θέλουμε να κάνουμε την μελέτη και έχει φορτίο τον κλάδο που εξετάζουμε. Διακρίνουμε δύο τύπους ισοδύναμων κυκλωμάτων: κατά Thevenin και κατά Norton.

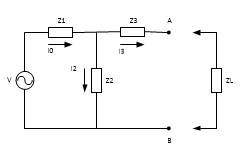
Σχήμα 1. Κύκλωμα προς μελέτη

     Για το ισοδύναμο κύκλωμα κατά Thevenin στη θέση του κυκλώματος που αντικαθιστάται, τοποθετείται ένα κύκλωμα που αποτελείται από μια πηγή τάσης και μια σύνθετη αντίσταση σε σειρά με την πηγή. Η τιμή της πηγής ονομάζεται τάση Thevenin (V_TH) και η τιμή της σύνθετης αντίστασης ονομάζεται αντίσταση Thevenin (Z_TH). Ο κλάδος αυτός έχει ακριβώς την ίδια συμπεριφορά στο φορτίο που θα είχε και το αρχικό κύκλωμα. Παρακάτω θα περιγράψουμε τη μεθοδολογία της αντικατάστασης κατά Thevenin για ένα απλόκύκλωμα.

    Έστω ότι στο κύκλωμα του σχήματος 1 θέλουμε να μελετήσουμε τα χαρακτηριστικά του φορτίου (Ζ_L). Θα αντικαταστήσουμε το κύκλωμα αριστερά από τα άκρα ΑΒ με ένα απλούστερο. Αρχικά αφαιρούμε τα φορτία. Αφαιρούμε επίσης όλες τις πηγές ρεύματος (εφόσον υπάρχουν) και ανοίγουμε το κύκλωμα στα σημεία εκείνα. Αντικαθιστούμε τις πηγές τάσης με βραχυκύκλωμα. Έτσι προκύπτει το κύκλωμα του σχήματος 2.

     Στη συνέχεια υπολογίζουμε την ολική αντίσταση των στοιχείων που απέμειναν. Αυτή είναι η αντίσταση Thevenin (Z_TH).  Για το κύκλωμα του σχήματος 2 είναι:

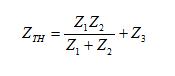
     Η τάση Thevenin (V_TH) είναι η διαφορά δυναμικού στα άκρα της αντίστασης Z₂ χωρίς να είναι το φορτίο συνδεδεμένο στα άκρα ΑΒ. Για το συγκεκριμένο κύκλωμα είναι:

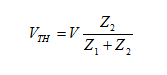
Σχήμα 2. Κύκλωμα που προέκυψε

Σχήμα 3. Ισοδύναμο κύκλωμα Thevenin

     Τέλος αντικαθιστούμε το ισοδύναμο κύκλωμα στο αρχικό σύμφωνα με τις τιμές που υπολογίσαμε (σχήμα 3).

     Για το ισοδύναμο κύκλωμα Norton στη θέση του κυκλώματος που αντικαθιστάται, τοποθετείται ένα κύκλωμα που αποτελείται από μια πηγή ρεύματος και μια σύνθετη αντίσταση συνδεδεμένη παράλληλα στην πηγή. Η τιμή της πηγής ονομάζεται ρεύμα Norton (I_N) και η τιμή της σύνθετης αντίστασης ονομάζεται αντίσταση Norton (Z_N). Το κύκλωμα αυτό έχει ακριβώς την ίδια συμπεριφορά στο φορτίο που θα είχε και το αρχικό κύκλωμα. Παρακάτω θα περιγράψουμε τη μεθοδολογία της αντικατάστασης κατά Nortonγια το κύκλωμα του σχήματος 1.

    Η μέθοδος υπολογισμού της αντίσταση Norton (Z_N) είναι ακριβώς η ίδια με την αντίσταση Thevenin (Z_TH). Αν έχουμε υπολογίσει και την τάση Thevenin (V_TH) το ρεύμα Norton (I_N) υπολογίζεται από τη σχέση:

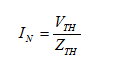
     Αν δεν έχουμε υπολογίσει την τάση Thevenin (V_TH) τότε για να υπολογίσουμε το ρεύμα Norton (I_N) αφαιρούμε το φορτίο και βραχυκυκλώνουμε τα άκρα ΑΒ. Το ρεύμα Norton (I_N) τότε είναι ίσο με το ρεύμα Ι₃ (σχ.1):

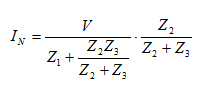
     Τέλος, αντικαθιστούμε το ισοδύναμο κύκλωμα στο αρχικό σύμφωνα με τις τιμές που υπολογίσαμε (σχήμα 4).

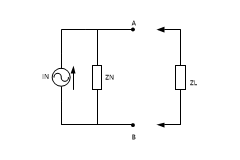
Σχήμα 4. Ισοδύναμο κύκλωμα Norton

       Σχήμα 5. Θεωρητικό κύκλωμα του                      πρώτου παραδείγματος

     Οι μέθοδοι επίλυσης και τα ισοδύναμα κυκλώματα που περιγράψαμε βρίσκουν εφαρμογή και σε συνεχή και σε εναλλασσόμενα ρεύματα με ωμικές η μιγαδικές αντιστάσεις. Στα επόμενα δύο παραδείγματα θα υπολογίσουμε τα ισοδύναμα κυκλώματα κατά Thevenin και Norton. Το θεωρητικό κύκλωμα του πρώτου παρουσιάζεται στο σχήμα 5.

     Σύμφωνα με τη διαδικασία που περιγράφουμε στις σελίδες 1 και 2 για να υπολογίσουμε την ισοδύναμη αντίσταση Thevenin (R_TH) βραχυκυκλώνουμε τις δύο πηγές τάσης και υπολογίζουμε την ολική αντίσταση του δικτυώματος που προκύπτει:

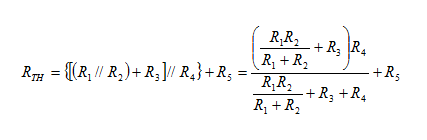
     Η τάση Thevenin (V_TH) είναι η τάση στα άκρα της R₄ χωρίς φορτίο συνδεδεμένο στα άκρα ΑΒ. Επειδή η R₅ δε διαρρέεται από ρεύμα, με τη μέθοδο των βρόχων έχουμε για το ρεύμα Ι_R4:

από όπου προκύπτει: V_TH=V_R4=I_R4R_R4

     Η αντίσταση Norton (R_N) είναι ίση με την αντίσταση Thevenin (R_TH). Το ρεύμα Norton (I_N) δίνεται από τη σχέση:

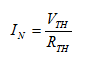
     Εναλλακτικά μπορεί να υπολογιστεί αν βραχυκυκλώσουμε τα άκρα ΑΒ και υπολογίσουμε το ρεύμα Ι_R5. Επιλύοντας με τη μέθοδο των βρόχων (με βραχυκυκλωμένα τα άκρα ΑΒ και για τον τρίτο βρόχο που σχηματίζεται φορά διαγραφής όμοια με των άλλων δύο) έχουμε για το ρεύμα Ι_R5:

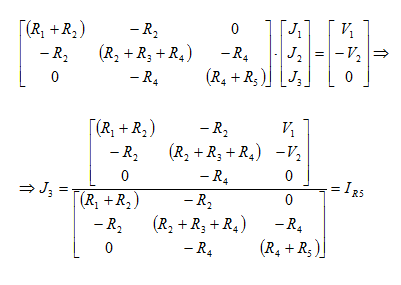
     Το θεωρητικό κύκλωμα του δεύτερου παραδείγματος παρουσιάζεται στο σχήμα 6.

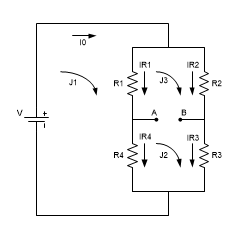
       Σχήμα 6. Θεωρητικό κύκλωμα του                      δεύτερου παραδείγματος

     Σύμφωνα με τη διαδικασία που περιγράφουμε στις σελίδες 1 και 2 για να υπολογίσουμε την ισοδύναμη αντίσταση Thevenin (R_TH) βραχυκυκλώνουμε την πηγή τάσης και υπολογίζουμε την ολική αντίσταση του δικτυώματος που προκύπτει:

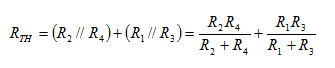
     Η τάση Thevenin (V_TH) είναι ίση με τη διαφορά δυναμικού στα άκρα των  R₃ και R₄ χωρίς φορτίο συνδεδεμένο στα άκρα ΑΒ. Η διαφορά δυναμικού μπορεί να βρεθεί από τις σχέσεις:

     Η αντίσταση Norton (R_N) είναι ίση με την αντίσταση Thevenin (R_TH). Το ρεύμα Norton (I_N) δίνεται από τη σχέση:

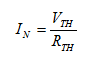
     Με άλλο τρόπο μπορεί να υπολογιστεί αν βραχυκυκλώσουμε τα άκρα ΑΒ και υπολογίσουμε το ρεύμα I_N=J₂-J₃. Επιλύοντας με τη μέθοδο των βρόχων (με βραχυκυκλωμένα τα άκρα ΑΒ και για τους τρεις βρόχους που σχηματίζονται με φορά διαγραφής όπως στο σχήμα 6) έχουμε για τα J₂, J₃:

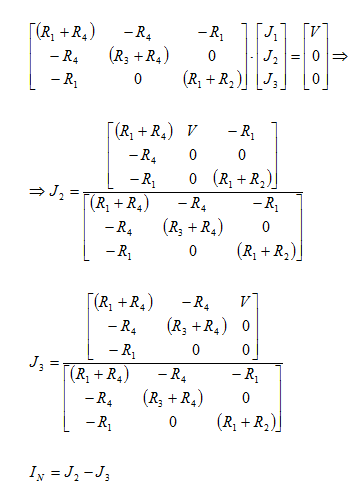
     Τα δύο κυκλώματα που μελετήσαμε μπορούν να αντικατασταθούν από τα ισοδύναμά τους κατά Thevenin ή Norton τα οποία είναι απλούστερα και έχουν ακριβώς την ίδια συμπεριφορά σε υποτιθέμενο φορτίο όποια και να είναι τα χαρακτηριστικά του. Τα ισοδύναμα κυκλώματα Thevenin και Norton έχουν τη μορφή των κυκλωμάτων των σχημάτων 3 και 4 αντίστοιχα. Η εφαρμογή αυτή ισχύει για συνεχή και για εναλλασσόμενα ρεύματα και για ωμικές και μιγαδικές αντιστάσεις χωρίς εξαιρέσεις.

Αρχείο .pdf για κατέβασμα

Σας ευχαριστώ για την υποστήριξή σας ώστε να γίνει η ιστοσελίδα μου καλύτερη.

© 2017 Πορλιδάς Δημήτριος