Επίλυση Κυκλωμάτων με τις μεθόδους των Βρόχων και των Κόμβων

     Η θεωρητική επίλυση ενός κυκλώματος μπορεί να γίνει εφαρμόζοντας τους νόμους του Kirchhoff στους βρόχους και τους κόμβους ενός κυκλώματος. Η μέθοδος αυτή μας οδηγεί στην επίλυση συστημάτων με πολλές εξισώσεις. Η επίλυση μπορεί να είναι αρκετά επίπονη όταν ο αριθμός των εξισώσεων αυξάνει. Με τις μεθόδους που θα περιγράψουμε στη συνέχεια ελαττώνεται ο αριθμός των εξισώσεων κατά μία ή κατά δύο κάνοντας την επίλυση ευκολότερη.

     Σχήμα 1. Θεωρητικό κύκλωμα προς            μελέτη με τη μέθοδο των βρόχων.

     Στο κύκλωμα του σχήματος 1 με τις κλασικές μεθόδους χρειαζόμαστε τουλάχιστο τέσσερις εξισώσεις για την επίλυσή του. Αρχικά θα μελετήσουμε την επίλυση του κυκλώματος με τη μέθοδο των βρόχων αφού πρώτα δώσουμε ορισμένους ορισμούς.

     Ορίζουμε ως κόμβο το σημείο που ενώνονται δύο η περισσότερα στοιχεία του κυκλώματος και ως κλάδο τη διαδρομή που συνδέει δύο κόμβους. Ο βρόχος κατά τη γνωστή έννοια είναι το κάθε κλειστό σύνολο κλάδων που μπορούμε ναδιατρέξουμε. Θεωρούμε ως ρεύμα βρόχου J_X το ρεύμα που διαρρέει τον βρόχο. Του ορίζουμε μια φορά διαγραφής την οποία συμβολίζουμε με μια ανοιχτή καμπύλη εσωτερικά του βρόχου. Το ρεύμα βρόχου J_X είναι ίσο με τοπραγματικό ρεύμα μόνο στα περιμετρικά μέρη του κυκλώματος ενώ γενικά μας βοηθάει στην επίλυση του κυκλώματος. Επίσης ορίζουμε και τη φορά των πηγών, όπως στο σχήμα 1. Ο αριθμός των εξισώσεων που θα προκύψει από τη μέθοδο αυτή υπακούει στη σχέση:

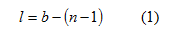
όπου l είναι ο αριθμός εξισώσεων, b ο αριθμός των κλάδων και n ο αριθμός των βρόχων. Το κύκλωμα του σχήματος 1 έχει πέντε κλάδους και δύο κόμβους και από τη σχέση (1) προκύπτει ότι θα χρησιμοποιήσουμε τρεις εξισώσεις, μία λιγότερη δηλαδή από τις κλασικές μεθόδους.

            Με βάση τη φορά διαγραφής των ρευμάτων  J_X  των τριών βρόχων (ΑΒΗΘ, ΒΓΖΗ, ΓΔΕΖ) και τις φορές των ρευμάτων  I_X  στις αντιστάσεις  Z_X , όπως σημειώνονται στο σχήμα 1, έχουμε τις παρακάτω σχέσεις για τα ρεύματα και τις τάσεις στις αντιστάσεις:

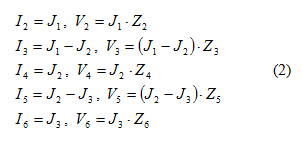
     Από το νόμο των τάσεων του Kirchhoff και με αντικατάσταση των τάσεων στις αντιστάσεις έχουμε:

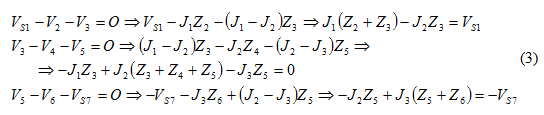
     Από τις σχέσεις αυτές προκύπτει το γινόμενο πινάκων:

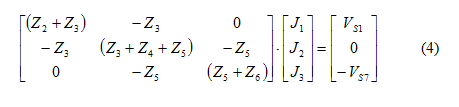
     Επιλύοντας ως προς  J₁ ,  J₂ ,  J₃ έχουμε:

     Με τη βοήθεια των σχέσεων (2) μπορούμε  να υπολογίσουμε στη συνέχεια τα ρεύματα και τις τάσεις για όλα τα στοιχεία του κυκλώματος.

     Ο πίνακας των αντιστάσεων της σχέσης (4) μπορεί να πάρει τη γενική μορφή [c_ij] όπου μόνο η κύρια διαγώνιος έχει θετικό πρόσημο και κάθε στοιχείο (c_ij) του πίνακα περιέχει το άθροισμα των αντιστάσεων του βρόχου (ij). Για παράδειγμα, το στοιχείο (c₁₁) περιέχει το άθροισμα των αντιστάσεων του πρώτου βρόχου, ενώ το στοιχείο (c₁₂) περιέχει το άθροισμα των κοινών αντιστάσεων του πρώτου και δεύτερου βρόχου. Ο πίνακας των τάσεων της σχέσης (4) μπορεί και αυτός να πάρει τη γενική μορφή [c_ij], όπου οι πηγές τάσης που έχουν ίδια φορά με τη φορά διαγραφής έχουν θετικό πρόσημο. Ο πίνακας των ρευμάτων  J_X είναι ο πίνακας των άγνωστων ρευμάτων.

     Σχήμα 1. Θεωρητικό κύκλωμα προς            μελέτη με τη μέθοδο των βρόχων.

     Σχήμα 1. Θεωρητικό κύκλωμα προς            μελέτη με τη μέθοδο των βρόχων.

     Στο παράδειγμα που ακολουθεί επιλύεται το κύκλωμα του σχήματος 2 με τη μέθοδο των βρόχων. Εφαρμόζοντας τη μέθοδο για τους δύο εμφανείς βρόχους και με φορά διαγραφής όπως εμφανίζεται στο σχέδιο του κυκλώματος του σχήματος 2 καταλήγουμε με βάση τη σχέση (4) στο γινόμενο πινάκων:

     Επιλύοντας ως προς  J₁ ,  J₂ ,  αφού αντικαταστήσουμε τις τιμές, προκύπτει ότι:

από όπου μπορούμε να υπολογίσουμε τα ρεύματα που διαρρέουν τον κάθε αντιστάτη:

       Σχήμα 2. Θεωρητικό κύκλωμα προς            επίλυση με τη μέθοδο των βρόχων.

     Σχήμα 3. Θεωρητικό κύκλωμα προς          επίλυση με τη μέθοδο των βρόχων.

     Στο παράδειγμα που ακολουθεί επιλύεται το κύκλωμα του σχήματος 3 με τη μέθοδο των βρόχων. Εφαρμόζοντας τη μέθοδο για τους τρεις εμφανείς βρόχους και με φορά διαγραφής όπως εμφανίζεται στο σχέδιο του κυκλώματος καταλήγουμε με βάση τη σχέση (4) στο γινόμενο πινάκων:

     Επιλύοντας ως προς  J₁ ,  J₂ ,  J₃ ,  αφού αντικαταστήσουμε τις τιμές, προκύπτει ότι:

από όπου μπορούμε να υπολογίσουμε τα ρεύματα που διαρρέουν τον κάθε αντιστάτη:

     Στη συνέχεια θα μελετήσουμε την επίλυση κυκλώματος με τη μέθοδο των κόμβων όπου οι εξισώσεις ελαττώνονται κατά μία ακόμα, κάνοντας έτσι πιο εύκολη την επίλυση του κυκλώματος. Στο σχήμα 4 δίνεται το θεωρητικό σχέδιο του κυκλώματος που θα μελετήσουμε. Το κύκλωμα αυτό έχει τρεις κόμβους από τους οποίους διαλέγουμε τον έναν και χαρακτηρίζουμε αυθαίρετα το δυναμικό του ίσο με μηδέν (γείωση του σχήματος). Τα υπόλοιπα δυναμικά δίνονται ως διαφορά προς αυτόν.

     Με βάση τις φορές των ρευμάτων  I_X  στις αντιστάσεις  Z_X  όπως σημειώνονται στο σχήμα 4, έχουμε από το νόμο των κόμβων του Kirchhoff, τις παρακάτω σχέσεις για τα ρεύματα στις αντιστάσεις:

     Αντικαθιστώντας στις παραπάνω σχέσεις τα ρεύματα  I₁ ,  I₂ ,  I₃ ,  από τις τάσεις  V₁ ,  V₂  και τις αγωγιμότητες  G₁ ,  G₂ ,  G₃ , σύμφωνα με το νόμο του Ohm, έχουμε:

     Από τις σχέσεις αυτές προκύπτει το γινόμενο πινάκων:

     Επιλύοντας ως προς  V₁ ,  V₂  μπορούμε να υπολογίσουμε στη συνέχεια τα ρεύματα και τις τάσεις για όλα τα στοιχεία του κυκλώματος:

     Ο πίνακας των αγωγιμοτήτων της σχέσης (16) μπορεί να πάρει τη γενική μορφή [c_ij] όπου μόνο η κύρια διαγώνιος έχει θετικό πρόσημο και κάθε στοιχείο (c_ij) του πίνακα περιέχει το άθροισμα των αγωγιμοτήτων του κόμβου (ij). Για παράδειγμα το στοιχείο (c₁₁) περιέχει το άθροισμα των αγωγιμοτήτων που συνδέονται στον πρώτο κόμβο, ενώ το στοιχείο (c₁₂) περιέχει το άθροισμα των κοινών αγωγιμοτήτων του πρώτου και δεύτερου κόμβου. Ο πίνακας των ρευμάτων της σχέσης (16) μπορεί και αυτός να πάρει τη γενική μορφή [c_ij] όπου οι πηγές ρεύματος που εισέρχονται στον κόμβο έχουν θετικό πρόσημο. Ο πίνακας των τάσεων V_X  είναι ο πίνακας των άγνωστων δυναμικών.

       Σχήμα 4. Θεωρητικό κύκλωμα προς              μελέτη με τη μέθοδο των κόμβων.

     Σχήμα 5. Θεωρητικό κύκλωμα προς         επίλυση με τη μέθοδο των κόμβων.

     Στο παράδειγμα που ακολουθεί επιλύεται το κύκλωμα του σχήματος 5 με τη μέθοδο των κόμβων. Για να επιλύσουμε το κύκλωμα με τη μέθοδο των κόμβων, ορίζουμε μηδενικό δυναμικό στον κάτω κόμβο, όπως φαίνεται στο σχήμα 5 και επειδή απομένει μόνο ένας κόμβος στο κύκλωμα, με βάση τη σχέση 16, το γινόμενο πινάκων παίρνει τη μορφή εξίσωσης:

     Αντικαθιστώντας τις τιμές στην παραπάνω εξίσωση προκύπτει ότι:  V= 4.06V  και  Ι_R2=V/R₂= 1.23mA. Από το νόμο των βρόχων του Kirchhoff για τον κάθε βρόχο και επειδή  Ι_R1=I_R3  και  Ι_R4=I_R5 έχουμε στη συνέχεια:

     Στο παράδειγμα που ακολουθεί επιλύεται το κύκλωμα του σχήματος 6 με τη μέθοδο των κόμβων. Για να επιλύσουμε το κύκλωμα με τη μέθοδο των κόμβων ορίζουμε μηδενικό δυναμικό στον κάτω κόμβο, όπως φαίνεται στο σχήμα 6. Για τους κόμβους Α και Β, με βάση τη σχέση (16), καταλήγουμε στο γινόμενο πινάκων :

     Αντικαθιστώντας τις τιμές στην παραπάνω εξίσωση και επιλύοντας ως προς  V_A , V_B  προκύπτει ότι:  V_A= 4.15V,  V_B= 2.47V,  από όπου μπορούμε να υπολογίσουμε τη διαφορά δυναμικού στα άκρα του κάθε αντιστάτη:

     Το ρεύμα που διαρρέει τον κάθε αντιστάτη υπολογίζεται από το νόμο του Ohm βάση της διαφοράς δυναμικού στα άκρα του και της τιμής της αντίστασής του.

       Σχήμα 6. Θεωρητικό κύκλωμα προς            επίλυση με τη μέθοδο των κόμβων.

Αρχείο .pdf για κατέβασμα

Σας ευχαριστώ για την υποστήριξή σας ώστε να γίνει η ιστοσελίδα μου καλύτερη.

© 2017 Πορλιδάς Δημήτριος