|
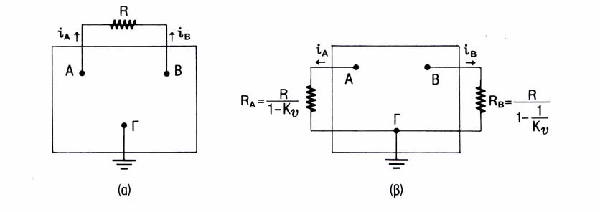
Σύμφωνα με το θεώρημα Miller, όταν μια
αντίσταση τοποθετηθεί μεταξύ δύο σημείων Α και Β αυτή μπορεί να αντικατασταθεί
ισοδύναμα με δύο αντιστάσεις από τα Α και Β προς τη γείωση. Το μέγεθος των
αντιστάσεων εξαρτάται από την απολαβή σύμφωνα με τις σχέσεις του παρακάτω
σχήματος. Για μεγάλες τιμές απολαβής η RB έχει τιμή περίπου ίση με την R,
ενώ η RA παρουσιάζεται
σημαντικά μικρότερη. Το θεώρημα ισχύει και για σύνθετες αντιστάσεις.
Στην περίπτωση που η αντίσταση μεταξύ
του κόμβου Α και Γ έχει χωρητικό χαρακτήρα έχουμε:
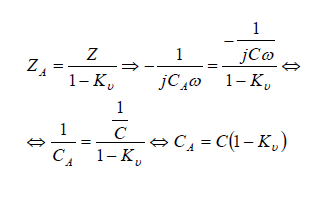
Επειδή στους ενισχυτές αναστροφής που
μελετάμε το κέρδος Κυ είναι η απολαβή Α του ενισχυτή και είναι αρνητικός
αριθμός έχουμε τελικά:
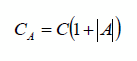
Όπου C ο πυκνωτής αντιστάθμισης και CA ο
ισοδύναμος κατά Miller πυκνωτής.
|