|
Όταν συνδέουμε ένα φορτίο σε κύκλωμα που παρέχει στην έξοδό του
μια τάση και έχει μια σύνθετη αντίσταση (κύκλωμα εξόδου), τότε μεταφέρεται
ισχύς από το κύκλωμα στο φορτίο. Η ποσότητα της ισχύος που θα μεταφερθεί και η
απόδοση της μεταφοράς ισχύος εξαρτώνται από την αντίσταση της πηγής και του
φορτίου και την τάση της πηγής. Ας υποθέσουμε ότι έχουμε ένα κύκλωμα, το οποίο αντικαθιστούμε με
ένα ισοδύναμο κύκλωμα Thevenin
με τάση στα άκρα του VTH και σύνθετη αντίσταση ΖΤΗ και συνδέουμε στα άκρα
του ένα φορτίο με σύνθετη αντίσταση ΖL.
Το ρεύμα I που διαρρέει το φορτίο ZL θα είναι ίσο με:
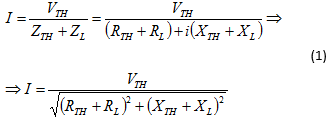
Η ισχύς PL που
προσφέρεται στο φορτίο RL θα είναι:
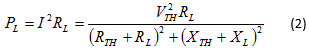
Αν υποθέσουμε ότι XTH = -XL τότε η
σχέση (2) που μας δίνει την ισχύ που προσφέρεται στο φορτίο RL γίνεται:
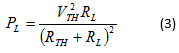
Η σχέση (3) ως συνάρτηση PL(RL) παρουσιάζει ακρότατα όταν μηδενίζεται η πρώτη παράγωγος,
δηλαδή όταν:

Το σημείο αυτό είναι
μέγιστο όταν η δεύτερη παράγωγος είναι αρνητική. Διερευνώντας τη δεύτερη
παράγωγο στο σημείο RL = RTH
βρίσκουμε:
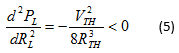
Καταλήγουμε λοιπόν στο
συμπέρασμα ότι όταν η αντίσταση φορτίου είναι ίση με την αντίσταση της πηγής
τότε έχουμε τη μεγαλύτερη μεταφορά ισχύος από την πηγή προς το φορτίο ή
γενικότερα από τη μια βαθμίδα στην άλλη εφόσον η πρώτη έχει το ρόλο πηγής
τροφοδοσίας και η δεύτερη το ρόλο φορτίου. Η μέγιστη ισχύ που μεταφέρεται σε
αυτήν την περίπτωση μπορεί να υπολογιστεί από τη σχέση (3) για RL = RTH:
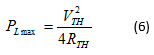
Η απόδοση του συστήματος
μεταφοράς δίνεται από το λόγο της ισχύος εξόδου Pout προς την
ισχύ εισόδου Pin, δηλαδή από την ισχύ που λαμβάνει το φορτίο PL προς την
ισχύ που προσφέρει η πηγή Pin, η οποία με την προϋπόθεση ότι ισχύει, XTH = -XL είναι:
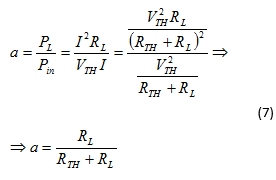
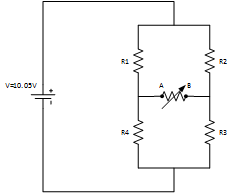
Σχήμα 1. Θεωρητικό κύκλωμα
του πειράματος.
Γιατην καλύτερη κατανόηση της μέγιστης μεταφοράς ισχύος εκτελέσαμε την παρακάτω πειραματική
διαδικασία. Συναρμολογήσαμε το κύκλωμα
του σχήματος 1 και μετρήσαμε με ηλεκτρονικό πολύμετρο την τάση VTH και την αντίσταση RTH στα άκρα AB χωρίς
να
συνδέσουμε φορτίο στο κύκλωμα. Οι τιμές αυτές είναι οι αντίστοιχες τιμές τάσης VTH και αντίστασης RTH σε ισοδύναμο κύκλωμα Thevenin. Στη
συνέχεια μπορούμε να θεωρήσουμε ότι το φορτίο συνδέεται σε ισοδύναμο κύκλωμα Thevenin και
αυτές τις τιμές θα χρησιμοποιήσουμε στους υπολογισμούς που θα κάνουμε. Η τάση
τροφοδοσίας ήταν V=10.05V, η τάση VTH μετρήθηκε VTH=1.687V και η
αντίσταση RTH μετρήθηκε RTH=1.356kΩ. Η
μέγιστη ισχύς που μπορεί να δώσει το κύκλωμα μπορεί να υπολογιστεί από τη σχέση
(6):
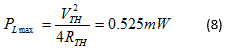
Οι ονομαστικές τιμές των
αντιστατών που χρησιμοποιήθηκαν παρουσιάζονται στον πίνακα Ι μαζί με τις
πραγματικές και τις αποκλίσεις από αυτές. Οι πραγματικές τιμές μετρήθηκαν με το
ηλεκτρονικό πολύμετρο.
Πίνακας Ι. Τιμές αντιστατών του κυκλώματος του σχ. 2.
|
α/α
|
Αντιστάτης
|
Ονομαστική τιμή (kΩ)
|
Πραγματική τιμή (kΩ)
|
Απόκλιση %
|
|
1
|
R1
|
1.5
|
1.481
|
1.3
|
|
2
|
R2
|
3.3
|
3.247
|
1.6
|
|
3
|
R3
|
1.0
|
0.994
|
0.6
|
|
4
|
R4
|
1.0
|
0.998
|
0.2
|
Στη συνέχεια συνδέσαμε κιβώτιο αντιστάσεων για φορτίο στα άκρα ΑΒκαι μετρήσαμε την τάση VL στα άκρα του για τιμές
αντιστάσεων από 100Ω ως 8kΩ.
Με βάση αυτές τις τιμές υπολογίσαμε από τη σχέση PL
= VL2 /
RL την ισχύ PL
που απορροφούσε το φορτίο και από τη σχέση (7) την απόδοση της μεταφοράς
ισχύος. Οι τιμές παρουσιάζονται στον πίνακα ΙΙ.
Πίνακας
ΙΙ. Απoρροφούμενη
ισχύς και απόδοση της μεταφοράς ισχύος για διάφορες τιμές
φορτίου.
|
α/α
|
RL
(kΩ)
|
VL
(V)
|
PL
(mW)
|
α%
|
|
1
|
0.101
|
0.156
|
0.241
|
06.9
|
|
2
|
0.504
|
0.456
|
0.413
|
27.1
|
|
3
|
0.704
|
0.575
|
0.470
|
34.2
|
|
4
|
1.008
|
0.718
|
0.511
|
42.6
|
|
5
|
1.103
|
0.756
|
0.518
|
44.9
|
|
6
|
1.156
|
0.775
|
0.520
|
46.0
|
|
7
|
1.206
|
0.793
|
0.521
|
47.1
|
|
8
|
1.258
|
0.810
|
0.522
|
48.1
|
|
9
|
1.308
|
0.826
|
0.522
|
49.1
|
|
10
|
1.356
|
0.843
|
0.524
|
50.0
|
|
11
|
1.407
|
0.857
|
0.522
|
50.9
|
|
12
|
1.458
|
0.872
|
0.522
|
51.8
|
|
13
|
1.510
|
0.887
|
0.521
|
52.7
|
|
14
|
1.708
|
0.938
|
0.515
|
55.7
|
|
15
|
2.014
|
1.007
|
0.504
|
59.8
|
|
16
|
2.515
|
1.094
|
0.476
|
65.0
|
|
17
|
3.014
|
1.162
|
0.448
|
69.0
|
|
18
|
3.517
|
1.215
|
0.420
|
72.2
|
|
19
|
4.020
|
1.259
|
0.394
|
74.8
|
|
20
|
4.520
|
1.296
|
0.372
|
76.9
|
|
21
|
5.020
|
1.326
|
0.350
|
78.7
|
|
22
|
5.520
|
1.352
|
0.331
|
80.3
|
|
23
|
6.020
|
1.374
|
0.314
|
81.6
|
|
24
|
6.520
|
1.394
|
0.298
|
82.8
|
|
25
|
6.920
|
1.408
|
0.286
|
83.6
|
|
26
|
7.540
|
1.426
|
0.270
|
84.8
|
|
27
|
8.030
|
1.440
|
0.258
|
85.6
|
Από τον πίνακα ΙΙ παρατηρούμε ότι μέγιστη μεταφορά ισχύος έχουμε
όταν η αντίσταση φορτίου RL
γίνει ίση με την ισοδύναμη αντίσταση RTH δηλαδή την αντίσταση εξόδου του κυκλώματος. Η τιμή αυτή είναι
ίση με την τιμή που υπολογίσαμε από τη σχέση (8) για τη μέγιστη ισχύ που μπορεί
να δώσει το κύκλωμα στο φορτίο (παρουσιάζει απόκλιση από τη θεωρητική τιμή
0.2%). Η απόδοση της μεταφοράς ισχύος στο σημείο της μέγιστης μεταφοράς είναι
50% και τείνει ασυμπτωτικά στο 100% όσο μεγαλώνει η αντίσταση φορτίου όπως
αποδεικνύεται και μαθηματικά από τη σχέση (7). Τη μεταβολή της ισχύος που
μεταφέρεται και την απόδοση της μεταφοράς σε σχέση με την αντίσταση φορτίου,
μπορούμε να παραστήσουμε γραφικά σε διάγραμμα (σχήμα 2).
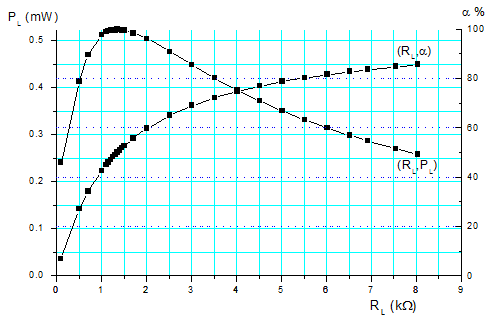
Σχήμα
2. Απoρροφούμενη
ισχύς και απόδοση της μεταφοράς ισχύος για διάφορες τιμές
φορτίου.
Το διάγραμμα είναι κανονικοποιημένο
με τέτοιο τρόπο ώστε ο αριστερός άξονας της ισχύος να έχει μέγιστο στο ίδιο ύψος
όπου ό δεξιός άξονας της απόδοσης έχει μέγιστο 100%. Από το διάγραμμα
παρατηρούμε ότι οι δύο καμπύλες τέμνονται στο σημείο που η απόδοση βρίσκεται
στο 75% και εκεί έχουμε τη βέλτιστη σχέση μεταφερόμενης ισχύος – απόδοσης. Στο
σημείο αυτό η αντίσταση φορτίου είναι RL=4.054kΩ και η
ισχύς PL=0.393mW.
|